Hace unos días tuve la ocasión de ver el último film de Christopher Nolan, Interstellar. Imagino que todos los lectores estarán al tanto de la temática del film, pero por si hay algún despistado hago un pequeño resumen.
Interstellar plantea un futuro no muy lejano en el que la población humana se ha visto drásticamente reducida debido a la escasez de alimentos. Esta escasez se debe a una serie de plagas que han eliminado prácticamente todas las plantaciones del planeta, de modo que los pocos supervivientes se ven obligados a buscar un nuevo comienzo lejos de la Tierra para no tener que comer buñuelos de maíz durante el resto de sus miserables vidas.
A partir de aquí, os lo podéis imaginar si no habéis visto la película: viajes interestelares buscando un nuevo hogar para la raza humana. En lo que esperamos sea una serie de entradas, vamos a repasar algunos de los conceptos relacionados con la ciencia que se ven en la película. En esta primera entrada explicaremos cómo funcionan los sistemas de gravedad artificial de las naves espaciales.
Para ello sólo hay que recordar las clases de física del instituto. En ellas todos vimos conceptos como la aceleración centrípeta y la fuerza centrífuga. Para los rezagados, vamos con una pequeña explicación.
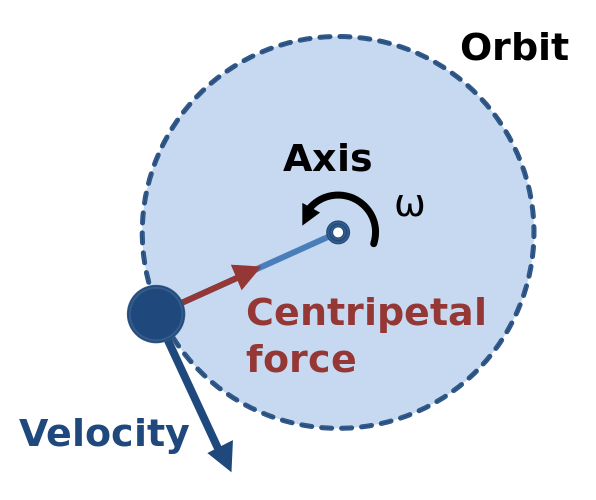
Cuando un cuerpo tiene un movimiento circular, este sufre la acción de una fuerza, denominada fuerza centrípeta, dirigida en dirección al centro de curvatura de la trayectoria que describe:
Un ejemplo de este fenómeno puede ilustrarse cuando un lanzador de martillo empieza a girar para realizar un lanzamiento en una competición. Como el peso está atado por medio de un alambre al lanzador, cuando este empieza a girar la bola sufre una fuerza (el alambre tira de la bola hacia el lanzador) que el lanzador es capaz de sentir. Seguro que en casa podéis hacer una prueba con algún cordel y una pequeña pelota o peso: cuando empecéis a girarlo notaréis como la pelota estira de vosotros (y por consiguiente, vosotros también estáis estirando de la pelota).
Ahora bien, esto es lo que nosotros veríamos, por ejemplo, si mirásemos ese objeto desde arriba (tal y como está en el esquema). ¿Qué pasa si nosotros estamos dentro de ese cuerpo, que se mueve en círculos?. En ese caso dejamos de estar en un sistema de referencia inercial (es decir, estamos en un sistema de referencia que tiene una aceleración no nula), y las cosas se vuelven un poco diferentes.
Para una persona que se sitúe dentro del cuerpo anterior (imaginemos que somos la pequeña pelota o el peso del martillo), aparece una fuerza hacia fuera de la órbita. Esta fuerza se denomina fuerza centrífuga. La fuerza cintrífuga puede sentirse muy fácilmente cuando se toma una curva en coche con algo de velocidad: enseguida sentimos que algo nos empuja hacia fuera de la curva.
Todo esto está muy bien, pero ¿qué tiene que ver con la gravedad artificial? Muy sencillo. Si vemos la nave que aparece en Interstellar, podemos observar que tiene una estructura anular en el borde, que es donde viven los tripulantes. Cuando la tripulación se coloca en ese anillo y este empieza a rotar, la fuerza centrífuga les empuja hacia fuera de la nave. Ahora bien, si esta está construida de modo que el círculo exterior del anillo es el suelo de la nave, ¡la fuerza centrífuga les empuja contra el suelo! Si pudiésemos controlar cuanta fuerza se aplica a los tripulantes, podríamos aplicar una fuerza igual a la gravitatoria en la superficie terrestre y estos no notarían que están flotando en el espacio.
Esta fuerza se puede controlar con distintos parámetros. Por una parte, el radio de curvatura que describe el cuerpo influye de forma inversamente proporcional (a menor radio, más fuerza). El otro parámetro es la velocidad de giro. Cuanto mayor sea esta, mayor será la fuerza centrífuga (por eso en un coche, cuanto más rápido tomamos la curva más notamos ese empuje hacia fuera). Como el radio de curvatura viene fijado por el diseño de la nave y no puede cambiarse una vez construida, el parámetro con el que podemos jugar (y es precisamente el que utilizan en la película) es la velocidad de rotación.
Para un cuerpo rotando, la aceleración centrípeta viene determinada por la relación:
donde es la velocidad lineal del objeto. Se puede expresar también en función de
, la velocidad angular. Hagamos un poco de matemáticas. Según la información que da The Science of Interstellar, la nave tiene un diámetro de unos 64 metros, esto es, un radio de 32 metros. Para generar los 9.8 m/s² terrestres, la nave necesitaría moverse a 17.7 m/s, o lo que es lo mismo, dar algo más de 5 vueltas por minuto (~5.3 vueltas/min) para simular la gravedad terrestre.
Ahora mismo no tengo acceso a la velocidad exacta que se ve en la película, pero haciendo un cálculo aproximado (a ojo) diría que lograron representar bastante bien la física necesaria para simular la gravedad terrestre en una nave espacial. Además, tal y como comentamos en una entrada anterior, estamos seguros de que los diseños anulares van a ser una realidad en un futuro cercano. En otra ocasión hablaremos de otros fragmentos del film y de la física detrás de ellos.