En esta entrega, voy a intentar explicar los fenómenos asociados al planeta de Miller (si, el de las olas gigantes) sin usar ni una sola ecuación. Veamos si soy capaz de hacerlo comprensible.
Cuando los tripulantes de la Endurance atraviesan el agujero de gusano, el primer planeta que deciden visitar es el planeta de Miller, que orbita alrededor de un gigantesco agujero negro (Gargantua). Este planeta tiene dos cosas curiosas. Por una parte, el tiempo en la superficie del planeta transcurre muchísimo más despacio de lo que los humanos tienen por costumbre (una hora en su superficie equivale a siete años terrestres). El otro fenómeno curioso es que en la superficie del planeta se generan unas olas gigantes (alrededor de un kilómetro de altura) que recorren toda la superficie. Bajo mi punto de vista, ambos sucesos están conectados y tienen que ver con la curvatura del espaciotiempo generada por la presencia de un objeto supermasivo (en este caso, el agujero negro). Abrochaos los cinturones que empieza lo bueno.
A comienzos del siglo XX, Albert Einstein desarrolló la teoría de la relatividad general. Sin entrar en mucho detalle, podría verse la relatividad general como una teoría que unifica los conceptos de la mecánica gravitatoria (es decir, las leyes del movimiento celeste) y la relatividad especial. La relatividad especial fue introducida, también por Einstein, unos años antes, y puede resumirse con la idea de que la velocidad de la luz en el vacío es la misma en cualquier sistema de referencia inercial que podamos imaginar, cosa que hasta ese momento no estaba nada clara. Uno de los conceptos relativistas más interesantes, bajo mi punto de vista, es el de espaciotiempo. El espaciotiempo consiste en considerar que el universo no solo tiene tres dimensiones (las tres dimensiones espaciales), sino que está formado por cuatro dimensiones (añadiendo el tiempo). ¿Qué implicaciones tiene esta consideración? Para empezar, al introducir el tiempo como una dimensión más, los fenómenos físicos afectarán tanto al espacio como al tiempo, lo que explica los fenómenos que vemos en Interstellar, que se deben a la curvatura del espaciotiempo.
Curvatura del espaciotiempo
Imaginemos el espacio como una red, donde los distintos cuerpos celestes pueden “colgarse”. Si miramos una zona vacía del espacio desde arriba, veríamos lo siguiente:
Las líneas que conforman la red serían las direcciones X e Y (dos dimensiones espaciales). Al mirar desde arriba a un solo plano, eliminamos la componente Z, y como estamos viendo un dibujo, también dejamos al margen el tiempo. ¿Qué ocurre cuando en lugar de espacio vació tenemos un objeto? Del mismo modo que al echar una canica sobre un trozo de tela esta se hunde, en el espacio tendríamos lo siguiente:
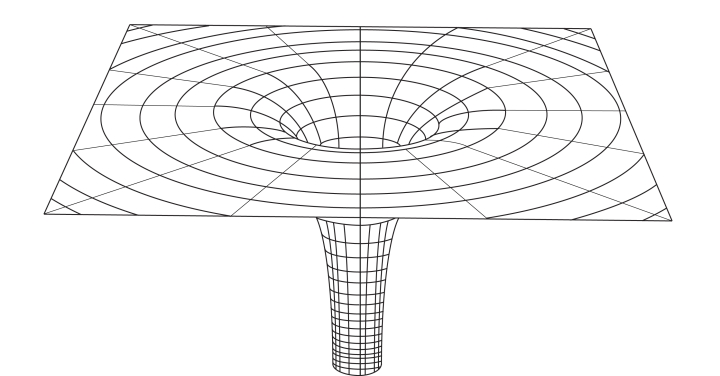
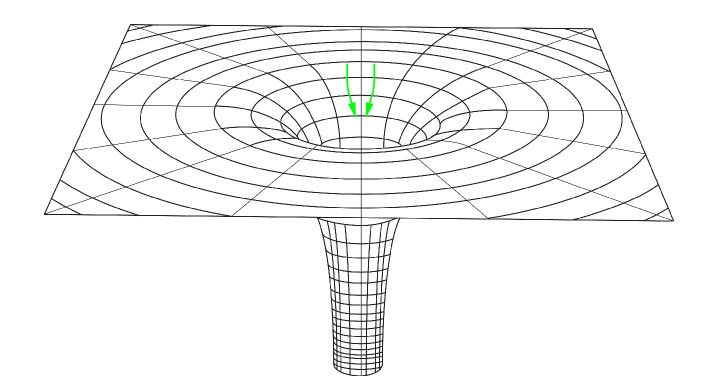
En la zona donde se encuentra el objeto (un planeta, una estrella, un agujero negro) la red se ve modificada, se curva. Esto es lo que se conoce como la curvatura del espacio, y es debida al campo gravitatorio que generan todos los cuerpos. Del mismo modo que un tejido se deforma más si sostiene una bola de bolos que si sostiene una canica, el espacio se curva en mayor medida alrededor de los objetos de mayor tamaño, como pueden ser las estrellas o los agujeros negros. Esto lo podemos ver a partir del siguiente esquema:
Como puede observarse, a medida que estamos más cerca del agujero negro, el espacio va curvándose cada vez más, debido a la abismal deformación provocada por la gran cantidad de masa que posee el agujero negro. Justo en el centro, el espacio se repliega sobre sí mismo en lo que se denomina singularidad. Estos ejemplos constituyen una forma intuitiva de entender la curvatura del espacio en dos dimensiones. Sin embargo, los conceptos pueden extrapolarse a la tercera dimensión espacial y al tiempo. En el caso del tiempo, esta curvatura provoca que el tiempo transcurra de forma diferente (se estira o se contrae, igual que el espacio) en zonas cercanas a objetos con mucha masa, como ocurre en el planeta de Miller.
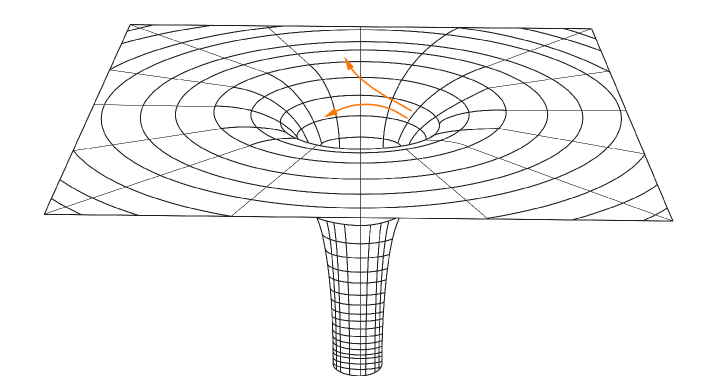
Ahora bien, ¿qué efectos tiene esta curvatura del espaciotiempo? Como decía antes, el tiempo comienza a pasar más despacio. Sin embargo, este no es el único efecto producido. Al curvarse el espacio, los objetos que están sobre él se ven afectados. Imaginemos que dos naves viajan cerca de un agujero negro, como en el esquema anterior. Ambas naves llevan trayectorias paralelas al principio, pero cada una se encuentra a una distancia distinta del agujero negro:
Las trayectorias que siguen las naves están pintadas en color naranja. Como guía visual, he coloreado un par de las líneas que conforman la red y he colocado dos cruces cuando las trayectorias cortan dichas líneas:
Como puede observarse, a medida que pasa el tiempo, las trayectorias se separan (las cruces cada vez están mas lejos). Si tenéis por casa un embudo y una canica o bola pequeña, podéis hacer la prueba lanzando la canica a distintas alturas, veréis como en unos casos la canica va hacia el fondo y en otros se escapa del embudo. Podría decirse que en un caso la bola queda atrapada por la curvatura del embudo y en el otro caso se escapa de esa curvatura. Para el caso de las naves espaciales, es lo mismo pero cambiando el embudo por el espaciotiempo.
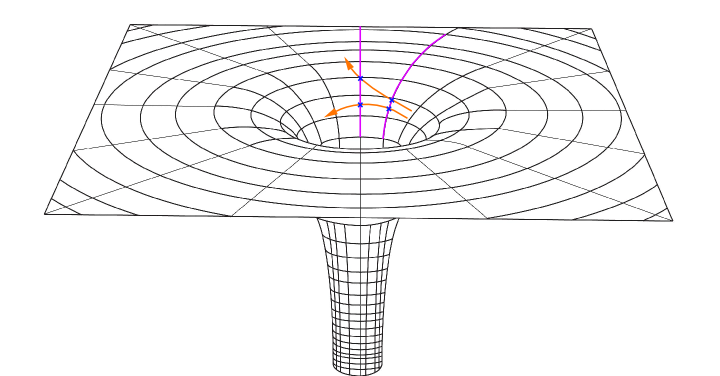
Imaginemos ahora otras dos trayectorias paralelas, en este caso pintadas de color verde.
Del mismo modo que antes, ambas trayectorias comienzan a desviarse, solo que ahora en lugar de separarse, tienden a juntarse (la distancia entre las cruces disminuye).
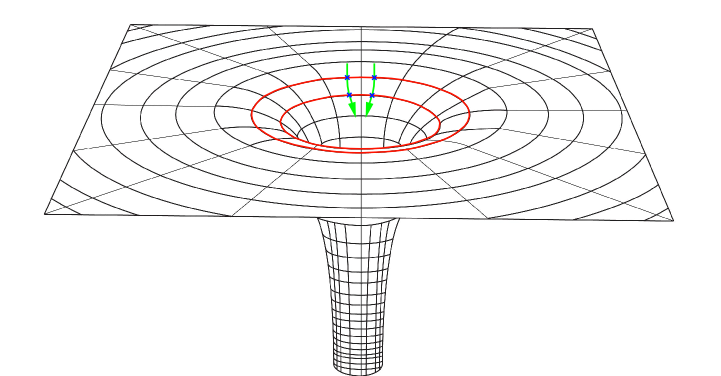
Estas líneas que he dibujado de color rojo y morado, se denominan tendex lines (del latín tendere, estirar). Son unas líneas imaginarias que se pueden dibujar saliendo o rodeando cualquier cuerpo que deforma el espaciotiempo e ilustran las fuerzas que sufren los cuerpos que se encuentran alrededor. Las líneas moradas, a medida que pasa el tiempo, hacen que las trayectorias se separen, es decir, hay una fuerza que estira a los cuerpos que se encuentran cerca del agujero negro. Por otra parte, las lineas rojas hacen que las trayectorias se junten, es decir, hay una fuerza que contrae a los cuerpos que se encuentran cerca del agujero negro.
Pero, ¿qué tiene que ver todo esto con Interstellar? Pues bien, tanto las olas gigantes como el retardo del tiempo son producidas por las tendex lines que genera el agujero negro, Gargantua.
Posiblemente muchos lectores estén familiarizados con las mareas terrestres. La explicación clásica de este fenómeno es que la Luna, al girar alrededor de la Tierra, genera fuerzas de atracción gravitatoria distintas en las diferentes partes del planeta, de modo que los mares se ven atraídos en mayor o menor medida por el satélite y el nivel del agua cambia. Ilustremos esta idea.
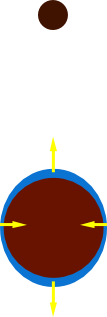
Esto va a ser nuestra Tierra, con su corteza y los mares por encima:
Ahora, consideremos que aparece la Luna. Como es bien sabido, la Luna ejerce una atracción gravitatoria sobre la Tierra, debido a su masa. Esta atracción actúa sobre todos los cuerpos del planeta, y va dirigida hacia el centro de la Luna. Por lo tanto, el agua que cubre la superficie terrestre se verá atraída en dirección al centro de la Luna:
Si descomponemos esas fuerzas en una componente común a toda la Tierra, más una parte distinta en cada punto, y restamos la parte común (si es igual en todos los puntos del planeta, somos incapaces de sentir esa fuerza), tendríamos un esquema tal que así:
Como el agua es un fluido, estas fuerzas hacia el centro del planeta o hacia el exterior provocan que la masa de agua se deforme, generando las mareas (que podemos ver al anochecer y al amanecer, cuando la Luna se “acerca” o se “aleja” de la costa).
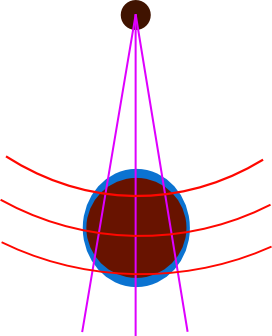
Ahora bien, en este último esquema vemos que hay dos fuerzas que estrujan el planeta por su centro, y dos fuerzas que lo estiran por arriba y por abajo, ¡igual que las fuerzas generadas por las tendex lines! Si consideramos la Luna como un cuerpo que deforma el espaciotiempo, podemos hacer este esquema:
Como he comentado antes, las lineas moradas estiran los cuerpos, mientras que las rojas, los contraen. Queda claro que la formulación proporcionada por la relatividad general es análoga a la gravitación clásica de Newton en este caso. Entonces, ¿por qué usar la relatividad, que resulta mucho más compleja? Pues la respuesta es bien sencilla. El otro fenómeno que vemos en Interstellar es la contracción temporal, y eso es algo que no está contemplado en la mecánica gravitatoria clásica, mientras que en la relatividad general, estas tendex lines, también contraen o dilatan el tiempo, explicando por qué el planeta de Miller, que orbita en las cercanías de un agujero negro, tiene un transcurrir del tiempo mucho más lento que, por ejemplo, la Tierra.
Tal y como decía al principio de la entrada, estos efectos de deformación del espaciotiempo se deben al campo gravitatorio de los cuerpos celestes. A mayor masa, el campo gravitatorio generado por un objeto es mayor, por lo que este produce una deformación más apreciable. Por comparar, el campo generado por la Luna, que es un satétlite pequeño, es capaz de generar las mareas terrestres. Si en lugar de la Luna tuviésemos un cuerpo con una masa mucho mayor, las mareas serían mucho más intensas. En el caso extremo de un agujero negro (una masa increíblemente grande concentrada en una región extremadamente pequeña), la deformación es tan grande que los efectos de las mareas se verían multiplicados, hasta llegar a lo que podemos ver en Interstellar. Podemos concluir entonces, en que los fenómenos que vemos en la película tienen una base científica aceptada, cosa poco común en la actualidad viniendo de Hollywood.









Dios, sigue sin entrarme en la cabeza el tema de la relatividad del tiempo. Si el tiempo es una medida creada por el ser humano usando como referencia movimientos de los astros: un segundo es 1/60 de minuto, que a su vez es 1/60 de hora que a su vez es 1/24 de un día terrestre. No entiendo que en Interstellar el protagonista viaje a un planeta en el que una hora equivale a 7 años en La Tierra... ¡Si el tiempo es para todos el mismo! Entendería que me dijesen que envejeces más rápido o más lento debido a las condiciones del planeta o del ambiente espacial en el que estás, pero es que el tiempo es el mismo: 1 hora es 1/24 de vuelta de la Tierra alrededor de sí misma, y la Tierra como referencia la puedes tomar estando aquí o estando en otra Galaxia utilizando un reloj.
De verdad que no lo entiendo, y eso que me ha parecido muy interesante la imagen en la que planteas lo de la de las cuatro dimensiones y lo que sucede al acercarse al centro del agujero negro... Eso lo he entendido.
Ojalá me puedas resolver la duda, acabo de ver la película y me he quedado pensativa con eso de la relatividad del tiempo...
Un saludo.
Hola Luchikata. Pongamos por ejemplo un año. Un año es el tiempo que tarda la Tierra en dar una vuelta completa alrededor del Sol. Ahora bien, ¿qué pasa si desde la Tierra (donde estamos nosotros), esa distancia es distinta a la que vería alguien al lado de un agujero negro? Pues que esa persona tendría una definición de año diferente. Si esa persona ve las distancias más pequeñas de lo que las vemos nosotros, su año sería, del mismo modo, más corto que el nuestro. Por eso nosotros le veríamos envejecer más rápido, ya que mientras en la Tierra pasa un año, al lado del agujero negro pasa un año y algo más (dependiendo de como de curvado esté el espacio). La clave aquí es que no se pueden ver el espacio y el tiempo como entes separados, forman un todo. Se podría realizar el mismo razonamiento para los días, minutos y segundos, pero creo que es más fácil visualizarlo con el año (suele ser más sencillo ver traslaciones que rotaciones).
Se que puede parecer anti-intuitivo, y precisamente por eso tuvo tanto mérito formular esas teorías físicas.
Un saludo,
F. Soldevila
He leído esto por casualidad y me ha encantado. Estoy muy soprendida, no estoy familiarizada con estos temas pero lo has explicado tan bien que he entendido gran parte. Aquí tienes una leyente mas!! Enhorabuena.
Hola, no estoy del todo de acuerdo contigo, me explico, el planeta de Miller al estar tan cerca de gargantua tendría su rotación sincronizada con su traslación alrededor del agujero negro (gargantua), de forma que siempre mostraría la misma cara del planeta hacia el agujero negro ( lo mismo que ocurre entre la luna y la tierra ), esa sincronización haría que no hubieran olas, en todo caso, toda la masa de agua de ese hipotético planeta estaría situada en la cara que mira hacia el agujero negro, estando la otra parte del planeta sumido en la más absoluta de las oscuridades y por lo tanto con una temperatura tan baja que impediría que hubiese agua liquida.
un saludo
Yo el fallo argumental que le veo a la base científica de la peli es el siguiente no tiene tanto que ver con el funcionamiento de la relatividad en sí, sino con las magnitudes:
Para que una hora en la superficie del planeta, equivaliera a 7 años en la órbita, la gravedad del planeta tendría que ser descomunal. Los protas no habrían puesto un pie en el planeta así como si nada, habrían sido aplastados contra la superficie en un instante.
Ni siquiera tengo claro que la nave pudiese estabilizarse con esa facilidad en una órbita baja.
Tampoco tengo muy claro si esta deformación temporal en teoría se debe a la gravedad del planeta, de Gargantúa o ambos...
Admitámoslo: aunque la base científica es buena en el papel, no es creíble en la práctica.
Y me jode, porque me encanta Interstellar y deseo que todo esté bien hilado.
Lo que dices es totalmente correcto sino estuviese la presencia de Gargantúa y el planeta fuese mucho más pesado de lo que es en la película. Es el agujero negro quien deforma el espacio tiempo y hace que el tiempo pase mucho más lento con respecto a la tierra. La gravedad del planeta no será mucho mayor que la de la tierra dependerá de su peso pero quien ejerce esa distorsión en el espacio-tiempo a causa de su gravedad es la masa del ajugero negro supermasivo al cual está en órbita el planeta de Miller. Ten en cuenta que el planeta está a una cierta distancia (bastante lejos) del agujero negro. Cuanto más cerca estuviese el planeta del agujero negro, en el hipotético caso, más lento pasaría el tiempo ya que teóricamente en el centro de los agujeros negros ( la sigularidad) la deformación del espacio-tiempo es tal que el espacio y el tiempo dejan de existir tal y como los conocemos, las leyes físicas que rigen el universo como la relatividad general de Einstein y la física cuántica por si solas no permiten predecir que sucede una vez atravesado el horizonte de sucesos.
¿Pero la ola no es demasiado grande?...es decir, el agua les viene por poco más de la rodilla, ¿no hay suficiente masa de agua para generar la inmensa ola no?
Lo que yo quiero entender es que le llega el agua por las rodillas por el hecho de que toda la masa de agua está desplazada a la ola. Por lo menos así quiero entenderlo.
Un saludo
Lo de las olas gigantes podría explicarse también a una mayor velocidad de rotación del planeta. La Tierra en tiempos giraba más deprisa y se estima que olas de centenares de metros recorrían su superfície, casi lo mismo que ocurre en Miller, y si a eso le añadimos fuerzas gravitatorias bestiales nos sale un buen pastel.
Seg'un la fuerza gravitacional que aplica el agujero negro no entiendo por que desde el principio no los absorvio o qu etanta energia debieron requerir para que la nave no fuera devorada, además puede que en Miller tal ves no tocaban el fondo si no que flotaban debido a alta gravedad de gargantua?
Matemáticamente existe la posibilidad de que existan unos agujeros negros “benignos” a los que se podría entrar. Te animo a que leas el siguiente artículo. Matemáticamente podría ser, todo lo demás es ciencia ficción de momento 🙂
https://www.abc.es/ciencia/abci-hallan-posibilidad-entrar-vivos-agujero-negro-201802221643_noticia_amp.html
hooola angel, eres el de mi escuela?
Viendo tu correo electrónico, no creo
mmm...seguro?
como veo los correos de los que comentaron?
Hola desde 2024 Fernando, anoche vi por enésima vez la película y como siempre me quedé pillado en el planeta de Miller. He llegado a éste artículo de casualidad y entiendo perfectamente la explicación que diste hace años, además entiendo las dudas, pero nadie ha caído en un minúsculo detalle que hace imposible incluso aterrizar... "La Resaca" cuando estás en la orilla de la playa la resaca te entierra los pies literalmente. Pienso que la resaca de una ola gigante te tiene que estrujar contra la superficie o arrastrarte hacia su interior a una velocidad increíble. Pero bueno sigue siendo una película buenísima que sin duda volveré a ver. Por cierto es curioso que acaba de pasar una hora en el planeta de Miller. Un saludo Fernando, y también a todos los participantes que con sus dudas he resuelto las mías... Todos somos una hora más viejos que hace siete años.
¡Muchísimas gracias por tu comentario! Muy interesante lo que comentas.
¡Un abrazo!
Me he equivocado, llevamos una hora y cuarto aproximadamente...